どうも、こんばんは、オルソンです。
今回は、2024年8月16日放送のテレビ千鳥「テストで100点取りたいんじゃ!」に登場した大悟式計算法について書かせていただきます。
- 大悟式計算法とは?
漫才コンビ「千鳥」のボケ担当である山本大悟氏が、「テストで100点取りたいんじゃ!」という企画での力試しの計算問題において、計算問題を解きながらその場で考案した計算方法。
山本大悟氏は「テレビ千鳥」において、ときにMC、ときにプレイヤーとしてボケ、ツッコミ、例え、大喜利、企画力、さらには他の芸人へのコメントやフリなどお笑いやバラエティの面で卓越した思考力を持っていることに疑いの余地はなく、その活躍はテレビ千鳥のみにとどまっていないこともまた事実である。一方で、岡山県の離島育ちであるため、「島の教育をナメるな」と自嘲気味に言う通り、勉強はしてこなかったようで「フリップにひらがなのぬを書きたかったがド忘れした」、「ピカルの定理で綾部が意外とおバカというクイズ企画を根本から破壊しかけた」などのエピソードがある。
そんな山本大悟氏の相方である早川信行氏は、大悟式計算法を見て「阿呆ガリレオ」などと評していたが、最終的には正解する山本大悟氏を見て舌を巻いていた。
この記事では、そんな大悟式計算法の仕組みを暴き、山本大悟氏が偶然ではなく必然によって正解をもぎ取ったことを証明させていただく。
- 76×49

上の写真は大悟式計算法に基づく、76×49の筆算方法である。一度、皆さんには正しい(?)76×49の筆算を思い浮かべてもらいたい。
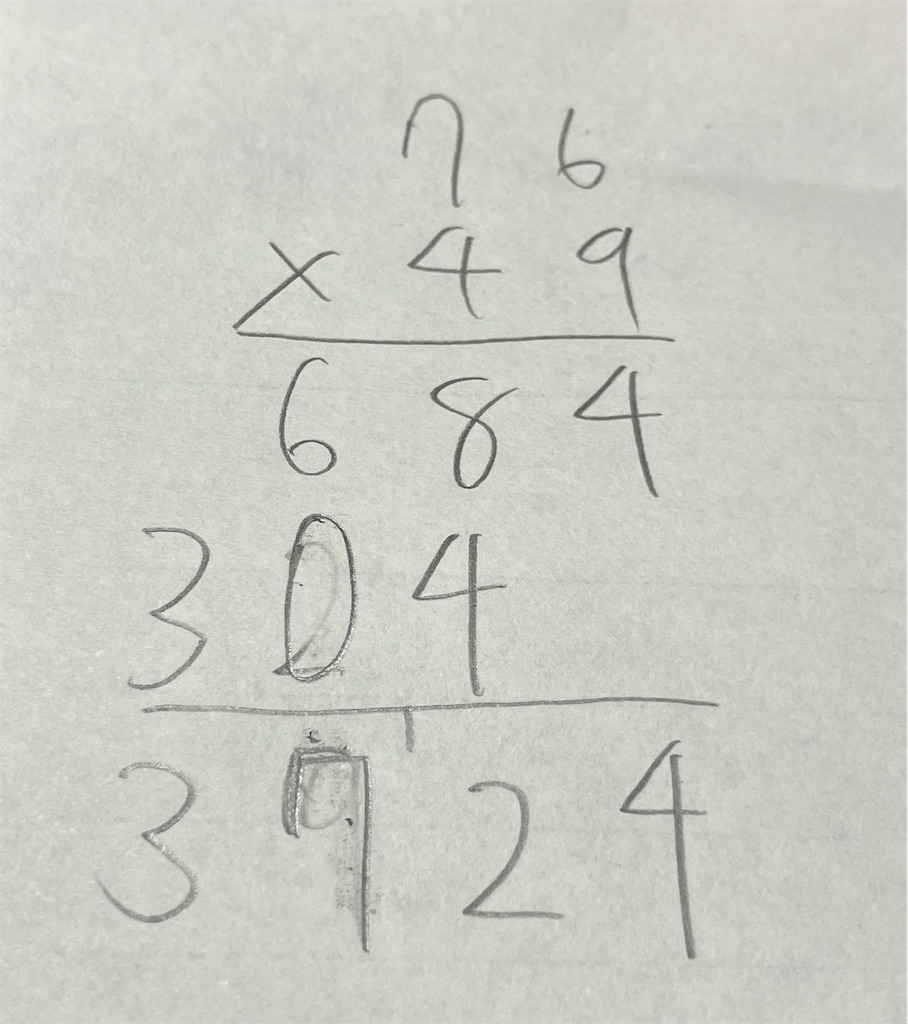
こうなるはずである。しかし、今こそ国民の皆様に問います。なぜ、76×4の答えを左に一個ズラすのでしょうか?そんなことも知らず、筆算を上の写真のように行い、やれ山本大悟氏を「島育ちの石屋の息子」、「阿呆ガリレオ」などとゲラゲラ笑いながらボーッと生きている国民の何と多いことか?しかし、オルソンちゃんは知っています。76×4をズラして書くのは、76×4ではなく76×40を計算しているから〜!!!
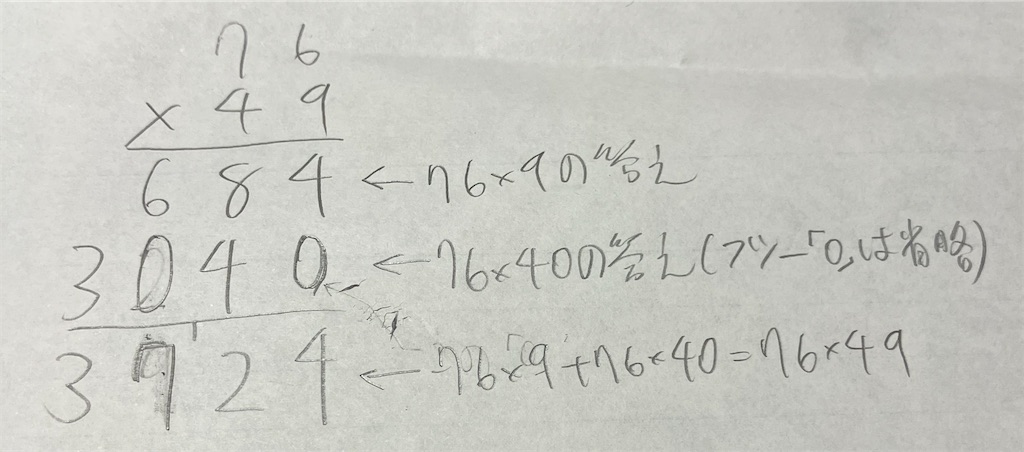
ということで、大悟式計算法を見返してみよう。

そう、山本大悟氏は自らがどの桁を計算しているかわかっているのである。

大悟式計算法は段数が嵩むうえに、ズラす桁に慣れが必要な一方、九九のみで完結させられるのが強みである。実際に計算方法を別の例で考えると、以下のようになる。
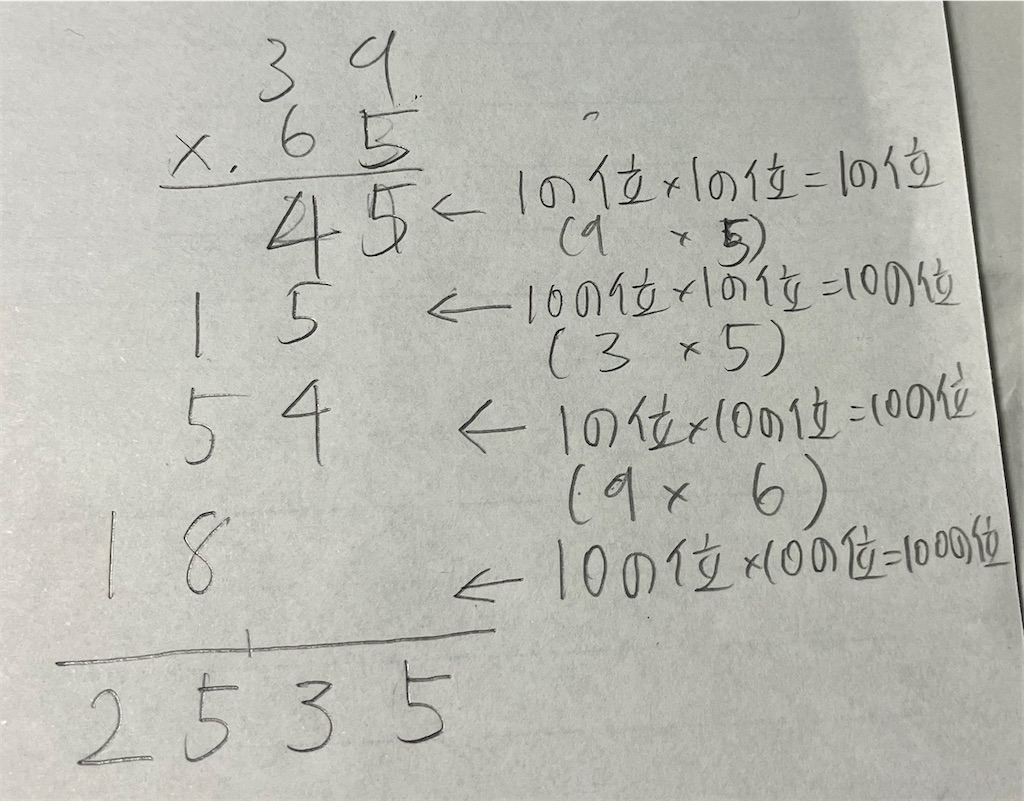
ズラす桁数を間違えなければ3桁×3桁だって自由自在だ(1回間違えたけど)。

- 1.7−9/10
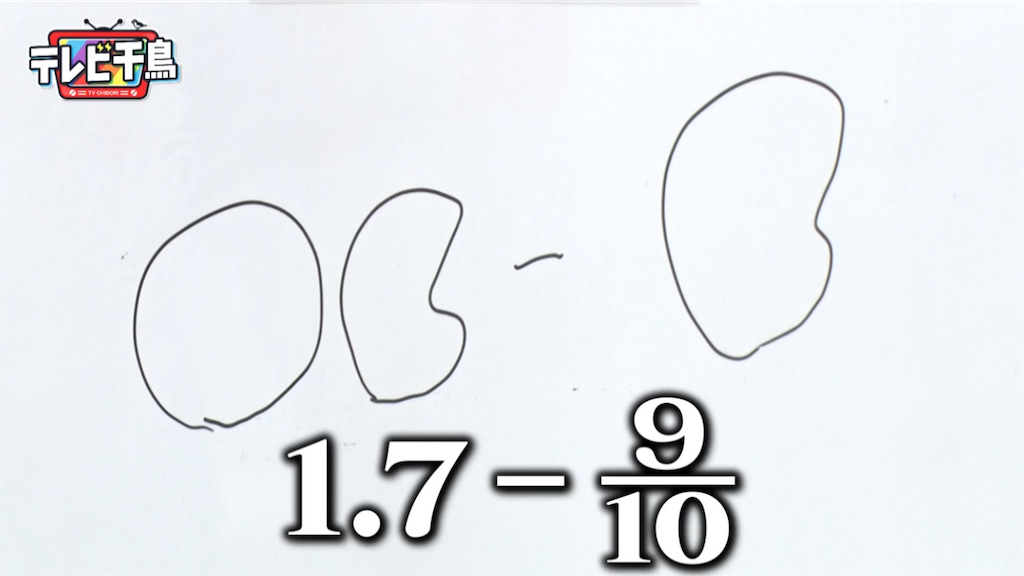
TVer版のサムネイルにもなっているが、こちらはフルーツポンチの村上健児氏の指摘通り「分数の本質」であろう。
1.7は17/10である。17/10の「10」というのは1個のパンケーキを10切れに分けたという意味である。そして「17」というのは切ったパンケーキが17切れあるという意味である*1。9/10も翻訳すると、下の写真のようになる。
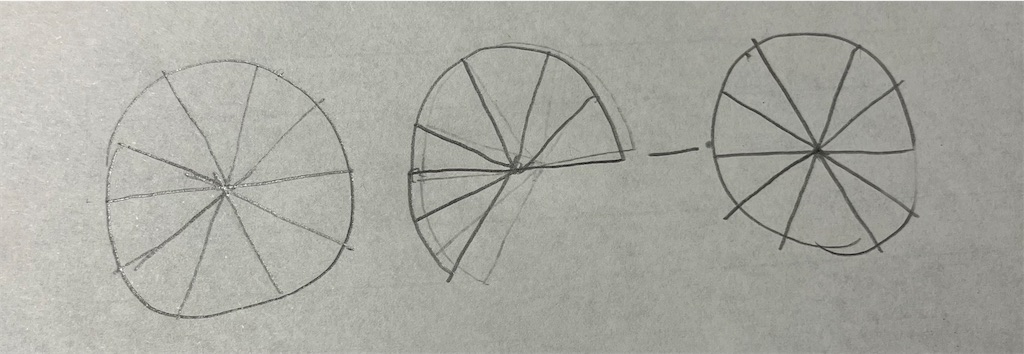
こうなると、「17切れあったパンケーキを9切れ食べると残りは何切れか?」という小学1年生レベルの問題に帰結する。よって、小数点は罠、分母は必要がないという山本大悟氏の考えが正しいことが証明されるのである。
惜しむらくは、山本大悟氏が分数の概念にパンケーキを用いてしまったことである。円形のパンケーキは分度器なしに大きさを正確に書くのが難しく、分数を把握するのには向いていない。
そのため、分母の異なる分数の計算は苦戦必至であり、実際に前編の次回予告の段階で苦戦している。山本大悟氏が線分図という概念を知っていれば…知らなかったとしても円形のパンケーキではなく、筒状のロールケーキで分数を計算していれば…より速やかに上の計算を処理できたはずなのである…。このパートは後編を見て、また追記します(注:結局、後編分はここと別パートとしました)
- 168÷6

こちらは、割り算の本質が引き算であることを知っていれば分かりやすいであろう。なお、割り算の本質が引き算であることは2008年センター試験数学ⅡBの選択問題「コンピュータと計算」にて出題されたことがある*2。

このように、168-6=162、162-6=156………と繰り返せば28回目には6-6=0となるため168÷6=28となる。もちろん、こんなことをやらないための割り算なのだが、大悟式計算法では、この引き算の数え方を多少なりとも効率化していると言える。その鍵が6×9=54である。つまり、上の写真と同様に、考えるとこうなる。

6×9=54は大悟氏が知っている6×◻︎の答えで最も大きいものであろう。大悟式計算法では掛け算に続いて、割り算をも九九のみで完結させようとしている。
ところで、168÷6では露呈しにくいが、そもそも現代の日本で広く使われている割り算の筆算には大きな欠点がある。それは、割り算をするには掛け算が必須ということである。
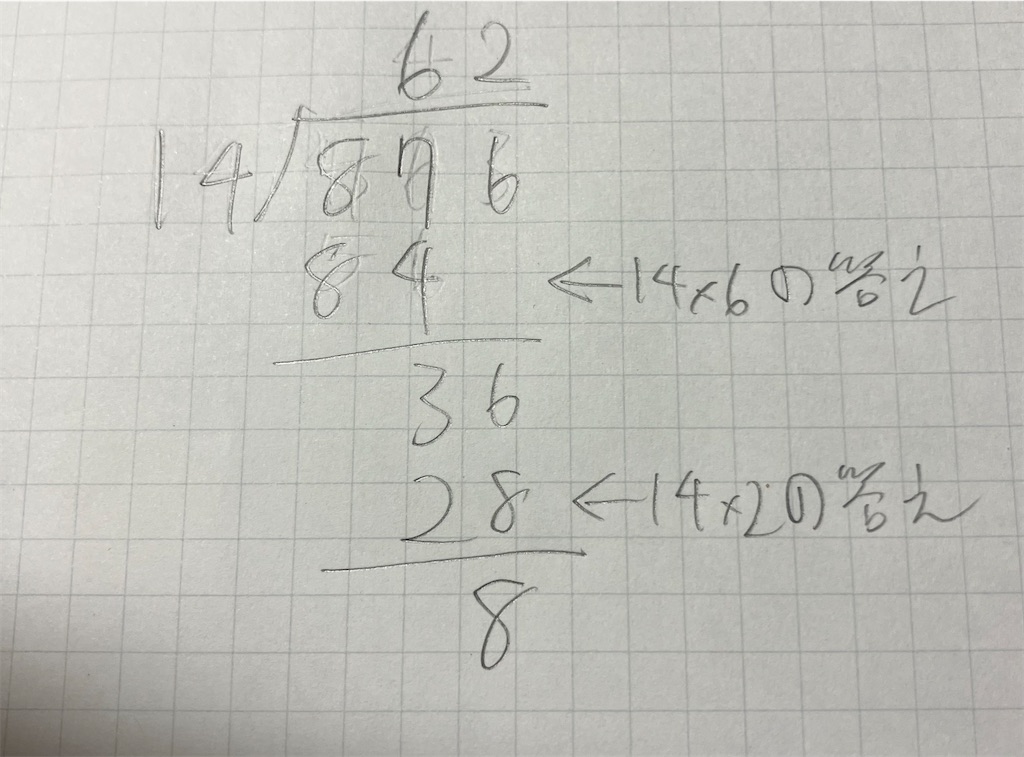
例えば、876÷14を筆算する場合、慣れていないと14×6も筆算することになる、というのは小学生の時に経験あるのではなかろうか?
そこで、大悟式計算法はこうだ。

×9ではなく×10を採用すれば、計算回数も桁が増えた時の計算も省力化できる。この点は私が勝手に改造しました。それはごめん。
- 1/3=なあなあ説
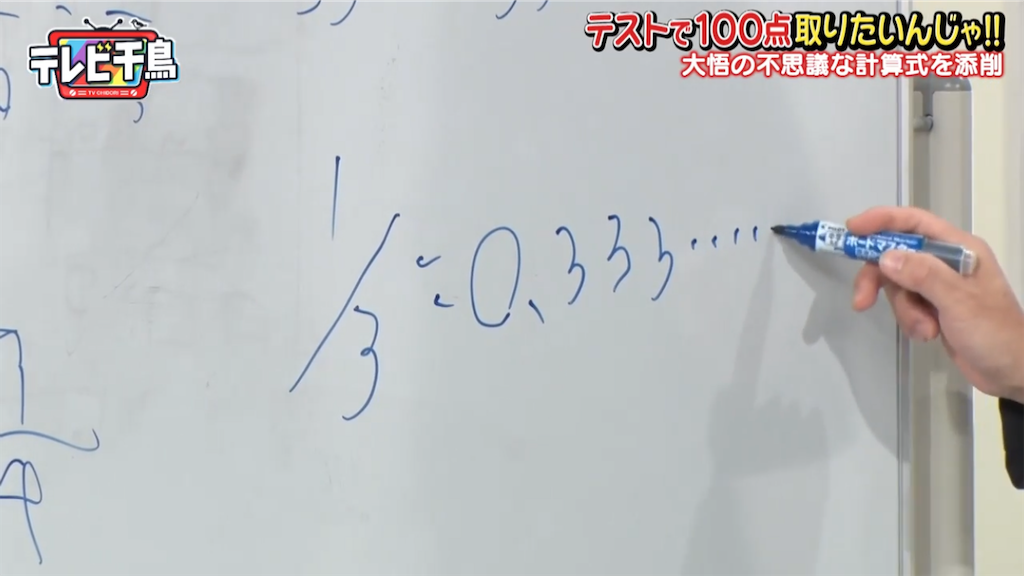

誰もがぶち当たる概念、1/3=なあなあ説。1/3
=0.3333……より、1/3×3=0.9999……≠1というのも有名な学説(?)である。この「なあなあ」というのは、極限という高校3年の数学で出てくる概念である。極限において出てくる「無限大」という概念が1/3×3=0.9999……=1たらしめている。無限大というのは本当に無限大である。例えば0.333…と3を1億個連ねても、その3倍は1ではなく0.999…と9が1億個連なった小数である。そう、無限大と言ったら一億よりも一兆よりも先、終わりなどないのということである。
よって、1/3=なあなあ説には高校3年範囲の数学が必要になる。村上氏が一旦教えるのをやめるのも無理はないということをご理解いただきたい。ただし、無限小数を分数にする方法自体は中学3年生の範囲となっている。
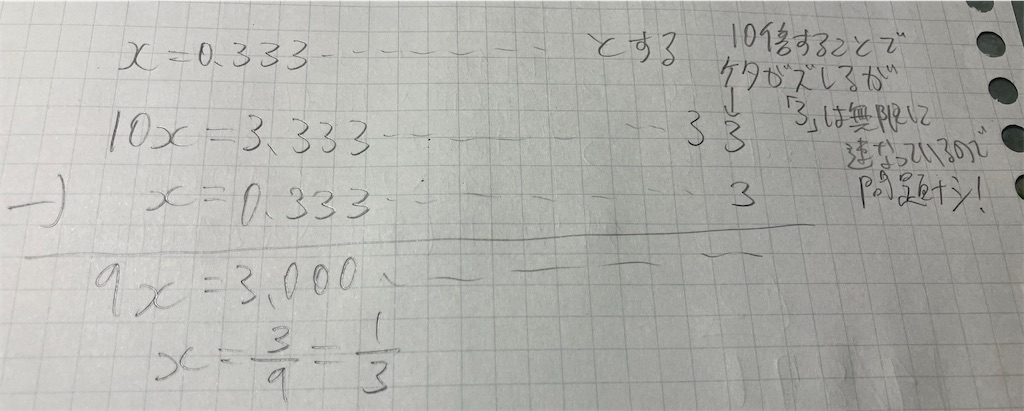
また、円の面積が半径×半径×円周率で導けることもまた、「なあなあ」改め「無限と極限」であることが知られている。
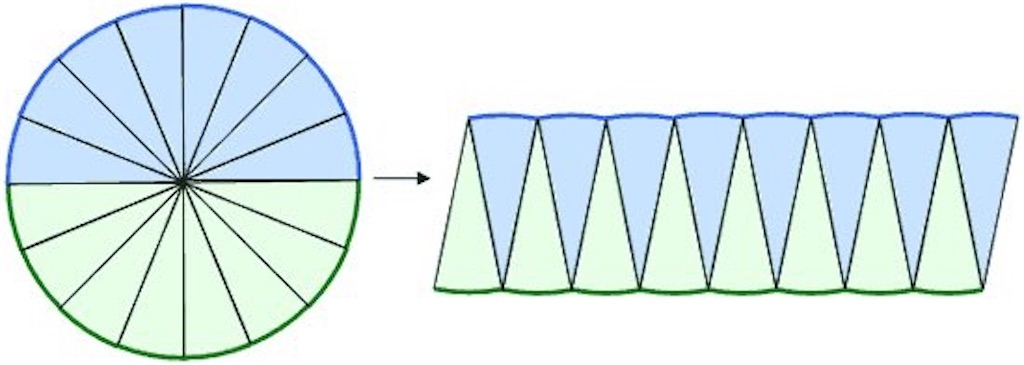
これだけ手書きじゃないのは力尽きたからです。無限に細かく円を刻んで上の図のようにすると縦が半径、横が円周の半分(直径×円周率÷2)の長方形になる。
数学と算数の違い、それは「なぜ?」という本質に迫り説明・思考するのか、操作方法を基礎として押さえて数字を当てはめる行為なのかの違い……なのかもしれない。
- 12−6.208
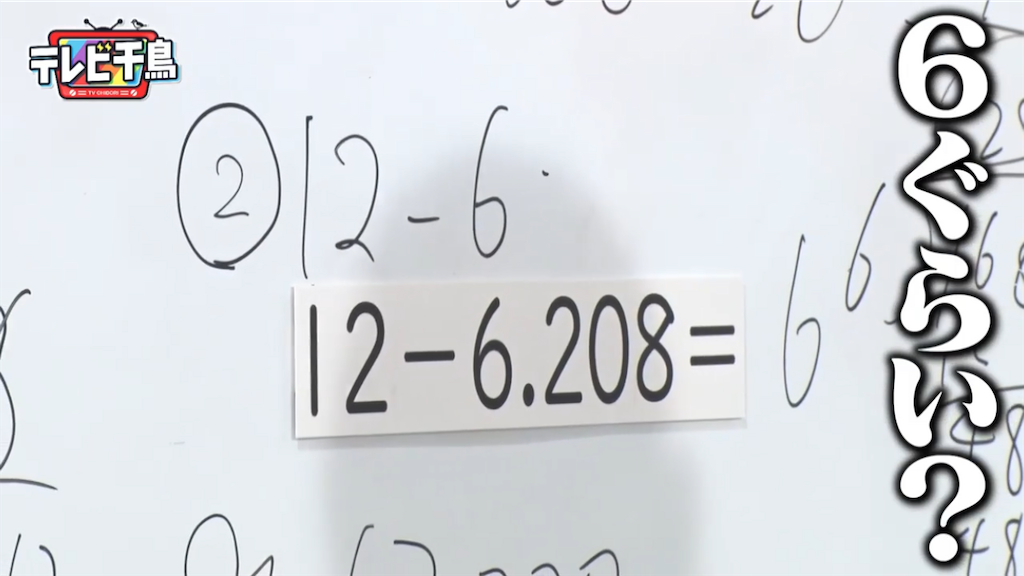
ここからは2024年8月23日放送分の後編である。「12−6.208」を見て、「6ぐらい」、「12−6が6やから、そこからちょっと抉れてんねん」と、式の第一印象を披露する山本大悟氏の感覚は確かで、こういう感覚があればそんなわけのない答えが出て、平気で計算終わりと言える生徒が多いことを思えば、大悟氏の勘には舌を巻かざるを得ない。
と、思いきや大悟氏本人がそんなわけない答えを出してしまうのだが…そこで軌道修正できるのもまた大悟式計算である。
そんな、大悟氏の計算であるが、これも一回正しい(?)12−6.208を見てみよう。こうなる。
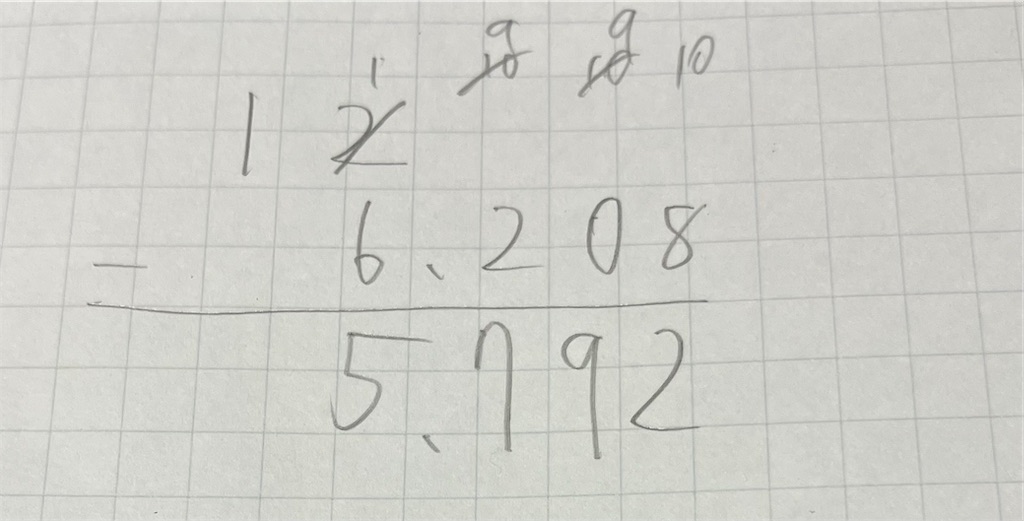
上の画像ではみなさんご存知、繰り下がりという手法が使われており、繰り下がりによって数字を減らしたり増やしたりすることでひとつの筆算で12−6.208を終わらせられる。
しかし、大悟式168÷6を思い出して欲しい。大悟式では、筆算のために新たな筆算が出てくることを躊躇わない。だから、整数部分と小数部分を分けて筆算するというパワープレイにより、小数の計算なのに小数点が出てこないというとんちのようなことを可能にしているのである。
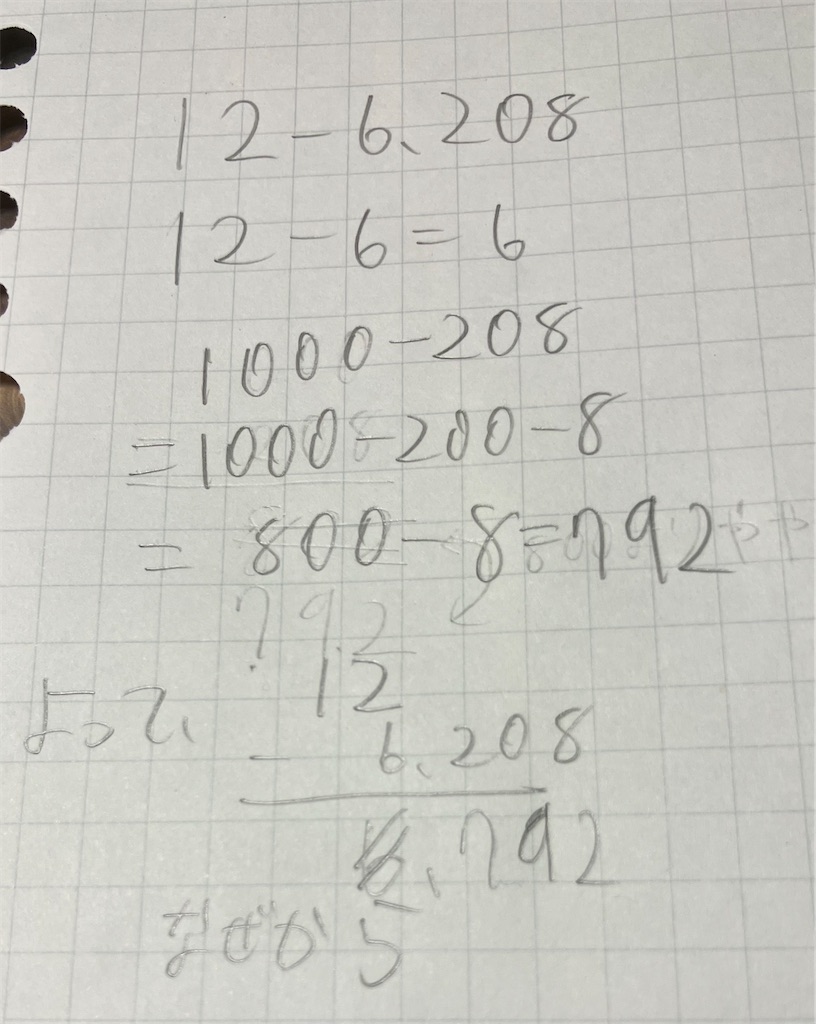
最後の最後に「なぜか」が出てくること以外は、本質的には我々の筆算と変わらない。だから、大悟式計算は当たるのである。
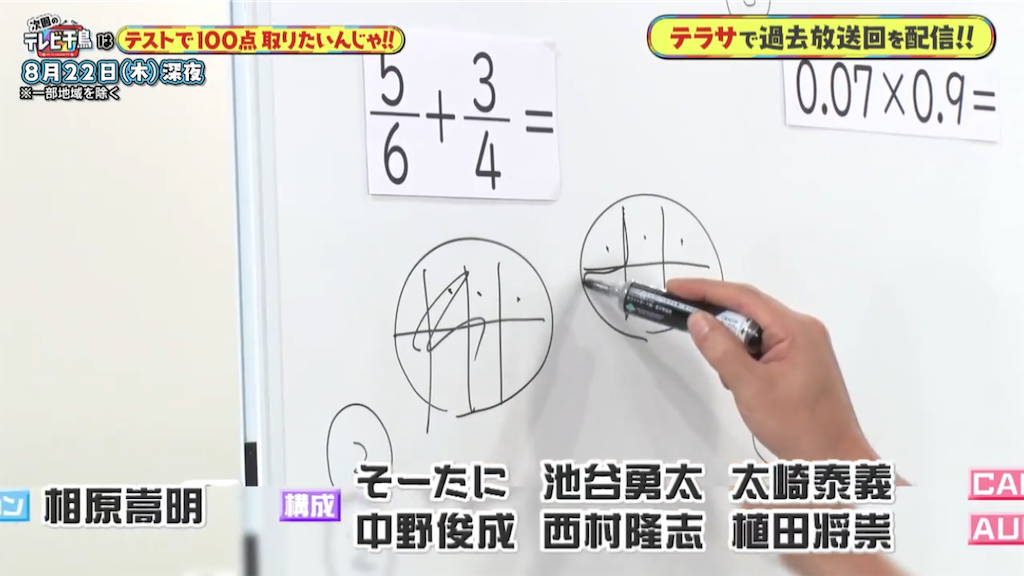
- 5/6+3/4
さあ、分母が異なる分数の足し算である。
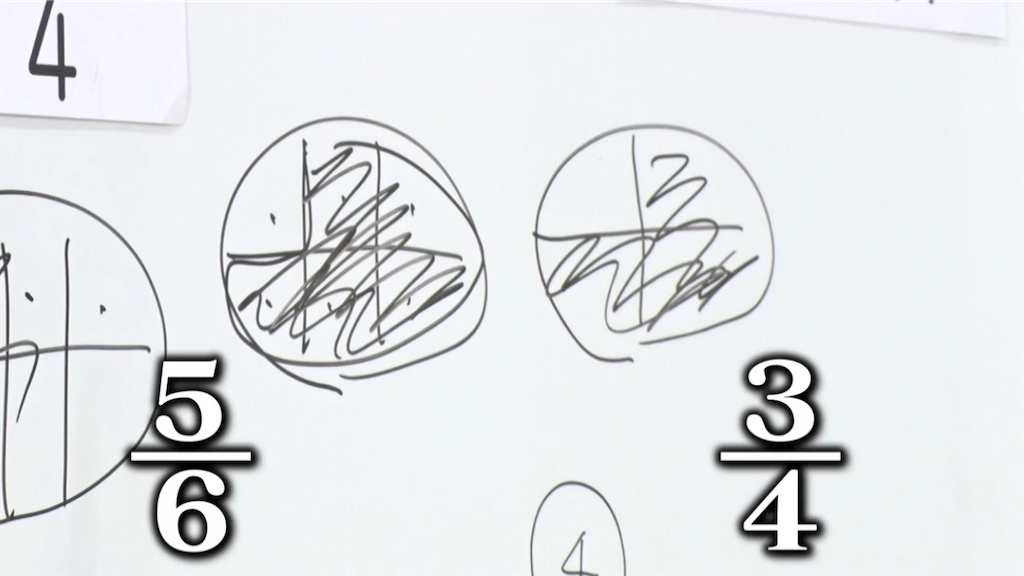
前編の次回予告にあった通り、大悟氏はパンケーキというよりオムライスな何かを分けて分数に見立てている。
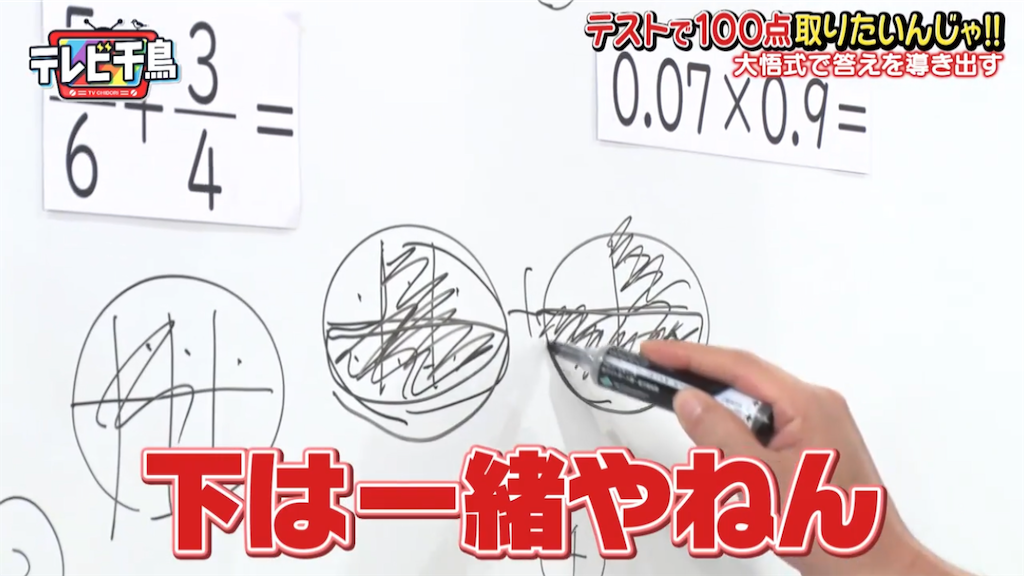
まず、大悟氏が辿り着いたこの概念。数式化すると以下のようになる。
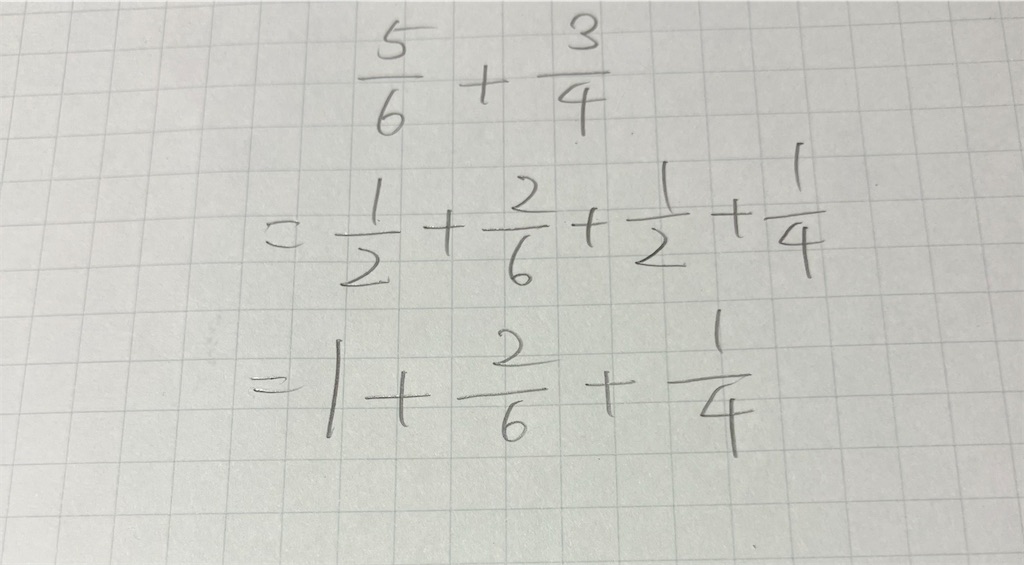
この方法により目指すべき計算が「2/6+1/4」となるという、ユークリッドの互除法を思わせる考え方だが、どれほど小さくしたところで分母が異なっていては足せないというところから逃げることはできない。
そこで、大悟氏は1/4+1/4=1/2としたうえで5/6からはみ出る部分、すなわち5/6−3/4を1/4の半分として近似。
端っこと真ん中が等しいはずもないということで、線分図ではなく平面を使って分数を表した弊害こそ出ているが、一方で、さほど的外れな近似でもないため、当たりこそしないが意外と近い値は出る。

その後、結局分母が揃っていないと足せないということにその場で自力で気づいた大悟氏は、分母を揃える方法を自力で編み出し、48分の…で計算する。下の画像の「お好み焼きを4個に分けた1切れと、8個に分けた2切れは量が一緒」というのも通分の本質そのものである。

その先、早川信行氏やスタッフから「でっかいやろ?」、「さっきの(通分の)逆」などヒントをもらい、正解に辿り着いたわけだが、実は分母を公倍数に揃える必要はあるが、最小公倍数である必要はない、ということを知っているのは、以下の計算を勉強することになる上でアドバンテージとなる。
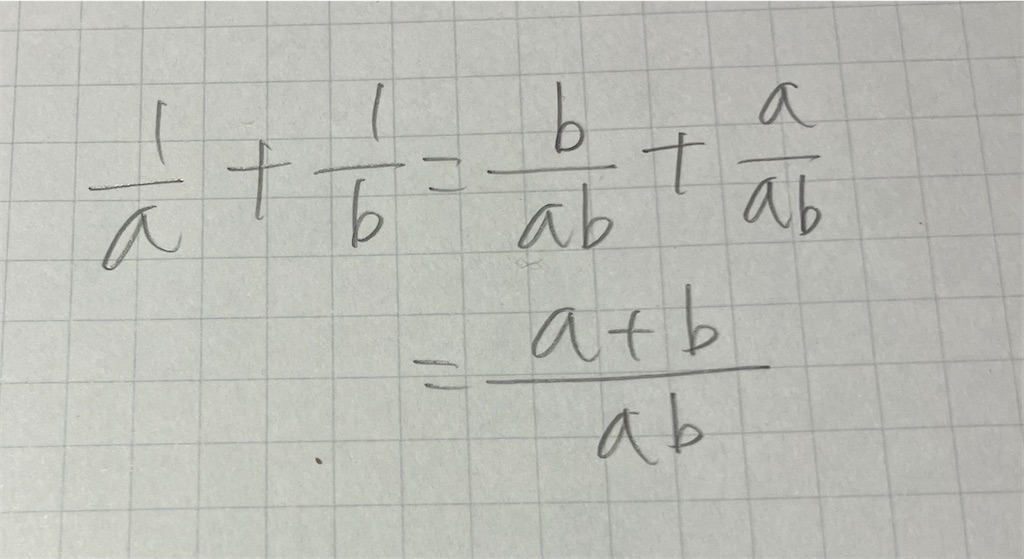
そう、5/6+6/8の分母を揃えるには6×8でよいと思っているのであれば、文字になったときも同様の操作でできるのである。本質がわかっていれば数字でも文字式でも同じ計算ができるはずであり、その点において、この収録を通して本質を理解した大悟氏は数学にも算数にも相当強いのである。
しかし、大悟式計算法では分数をパンケーキやお好み焼きなど平面で表すが、これは時間の都合でカットとなった小6算数では大きな枷となる。それは分数のかけ算での場合。
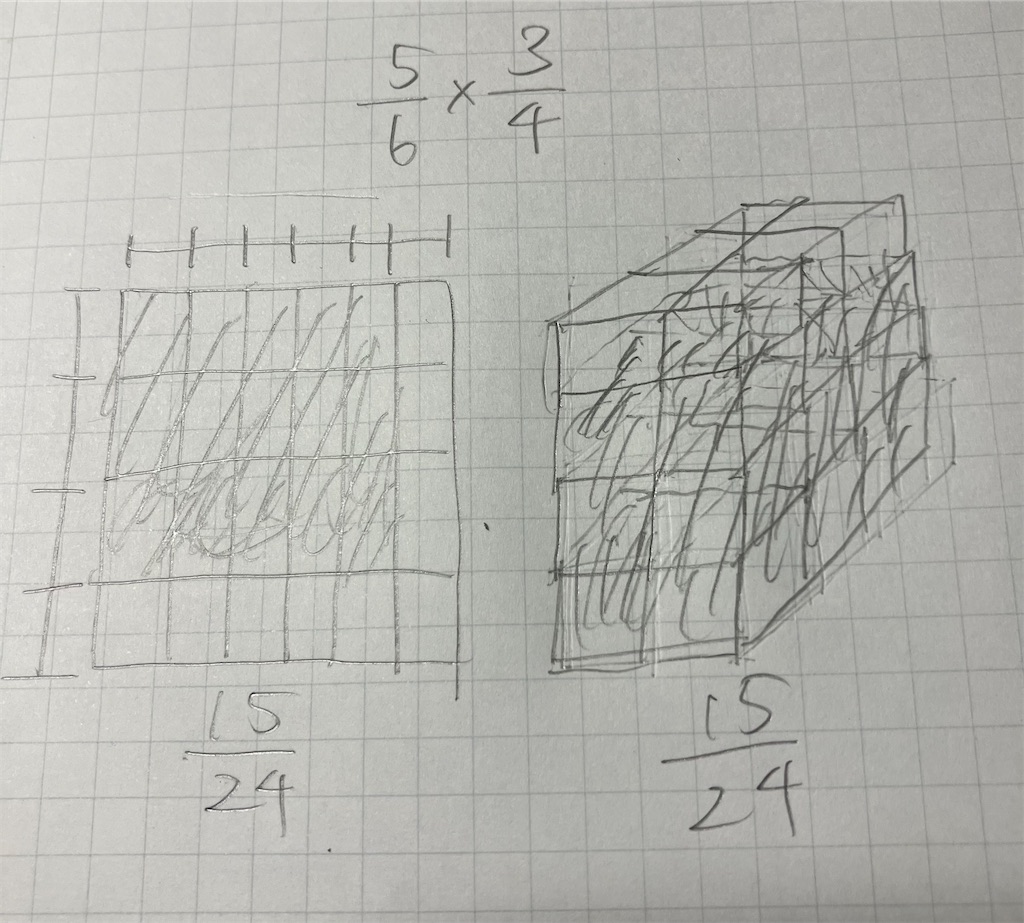
分数を一次元(線)で捉えれば、分数のかけ算は二次元(平面)で表されるが、分数を二次元(平面)で表すと分数のかけ算は三次元(立体)で表すことになってしまい、非常に見づらいということである。
- なぜテストに時間制限があるのか?
大悟「何でテストって時間制限してる?テストで時間制限するからみんな公式を覚えちゃうんやろ?本質を勉強しなくなったわけやん。今の学校教育ってどうなんだろ?」
ノブ「別のクラスに変えてください!進まないんですよ!」
番組最後のこのやりとりは、どちらも学校教育の本質を指しているように思う。
大悟式教育では現在小学校が6年やっている教育が10年、15年と伸びていくに違いない。現状の教育であれば、12年あれば小学一年生が三角関数の微積分をできるようになるのである。
さらに、テストになぜ制限時間があるのか?の答えもテレビ千鳥の問題中に用意してあったが皮肉にも収録の制限時間により消えてしまったように思う。
ツルとカメが合わせて7匹います。ツルとカメの足の本数を足すと全部で22本あります。ツルとカメはそれぞれ何匹いるでしょう?
これはテレビ千鳥側が最後に用意していたつるかめ算の問題である。一般的なつるかめ算の解き方は以下の通りである。

しかし、時間無制限であれば、ツルとカメが7匹であれば、以下のように全パターンを試してみるだけで当たってしまうし、パターンが8通りしかないので下のように順序立てずとも、時間が無限にあればいつかは当たってしまうような問題なのである。

このような問題に対して、全パターンを試さず手早い計算で当てられる*3というのが算数・数学がもたらす叡智である。つまり、少ない(と感じるかはテストの量と質、そして解く側の力次第だが)時間でどれほど問題を解けるか、というのがテストで測られる力である。速さもまた実力であり、テストに時間制限は必要なのである。
ただ、それはそれとして、ツルとカメの数を変えて行って最終的に「あっ!これあれや!ツル1匹をカメにしたら足が2本増えるんや!」と本質を発見をする山本大悟氏の姿は見たいので、また今度小6編、中学入試の特殊算もお願い致します。
(おしまい)
*1:サラッと、大悟氏が17/10=1.7に、おそらく自力で到達しているのも興味深い
*2:https://www.toshin.com/center/2008/sugaku-2b_mondai_6.html
*3:7匹だと少なすぎるが一般的な解法であれば100匹でも1000匹でも計算で解決する。一方、ツルとカメが100匹の場合、ツルとカメの数のパターンは101通りある